"CUDA Factor": A Library of Matrix Factorization routines
Harshavardhan Pandit and Ravi Chandra Bandlamudi
Writeup ::
Checkpoint ::
Proposal
Spring 2015 Parallelism Competition
Spring 2015 Parallelism Competition
Welcome to CUDA Factor - our project page for the Spring 2015 Parallelism Competition! This section provides a brief description of our project goals, deliverables and preliminary results. For a more detailed description, please visit the writeup section.
Summary
We have developed a library of GPU-accelerated optimized matrix factorization routines in CUDA. The routines currently implemented are:
- LU Factorization ( A = LU )
- QR Factorization ( A = QR )
- Cholesky Factorization ( A = LLT )
Results
At the competition, we would be showing a comparison of our library routines to the state-of-the-art libraries such as cuBLAS and CULA. Some preliminary results are shown below. Owing to well-tuned algorithms and their efficient implementation, we are able to beat the cuBLAS reference library by a huge margin, especially for higher matrix sizes. Our Cholesky routine performance is comparable to the CULA reference library for small matrix dimensions.
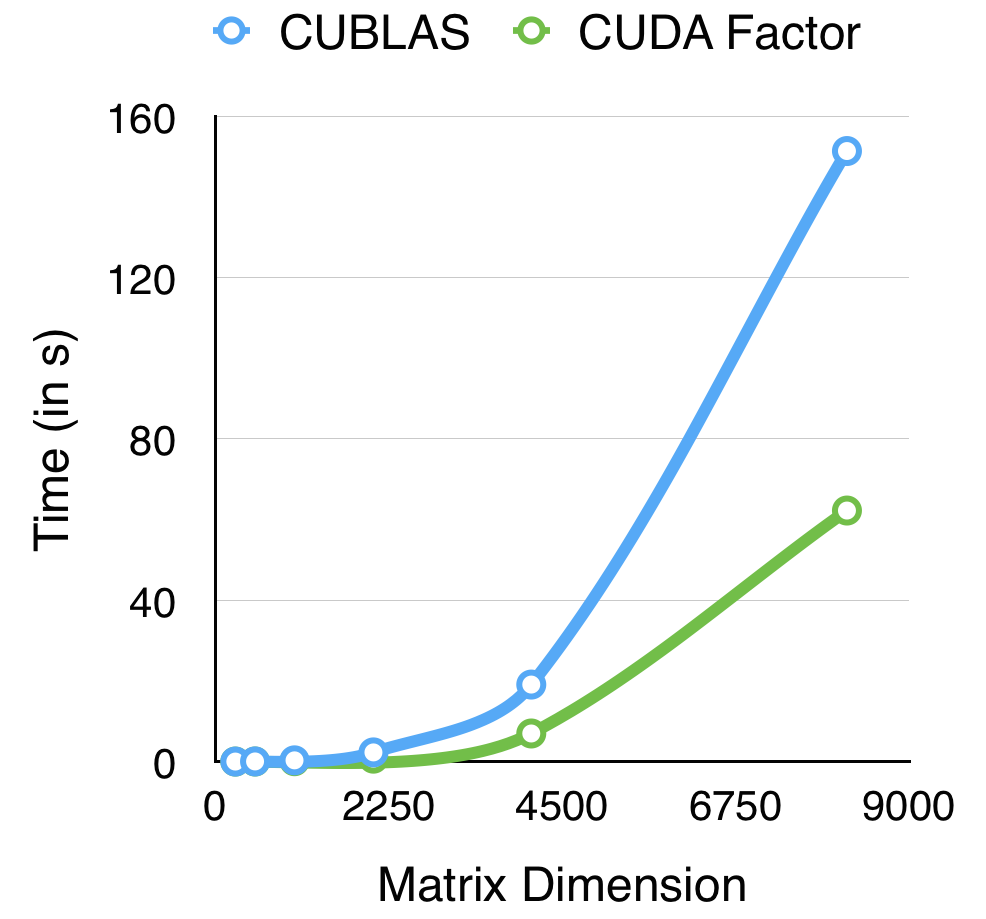
The following graph shows a comparison between our LU implementation and the cuBLAS reference when run on a GTX 670 GPU.
The following graphs show a comparison between our QR implementation and the cuBLAS reference when run on a Tesla K40 as well as a GTX 670 GPU. The cuBLAS QR routine is intended to be used for performing QR factorization on many small matrices in parallel, we have however focused on computing the factorization for one huge matrix as fast as possible. Such an use case is important as well, for instance, during PCA (Principal Component Analysis) calculations in Machine Learning/Pattern Recognition algorithms. Our performance is comparable to cuBLAS for smaller sizes and also scales better than the reference to higher matrix dimensions.
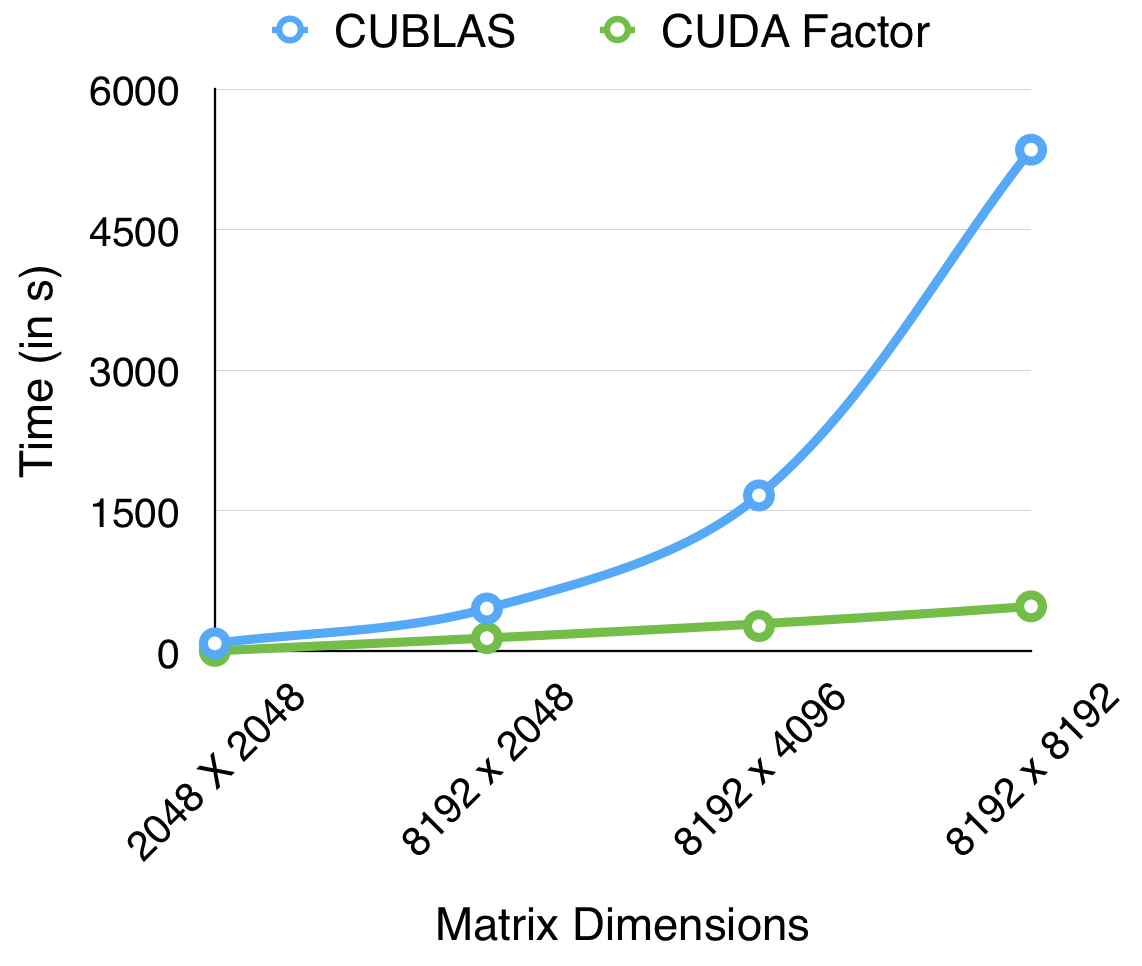
Performance of Our QR Routine on Tesla K40 Performance of our QR Routine on GTX 670
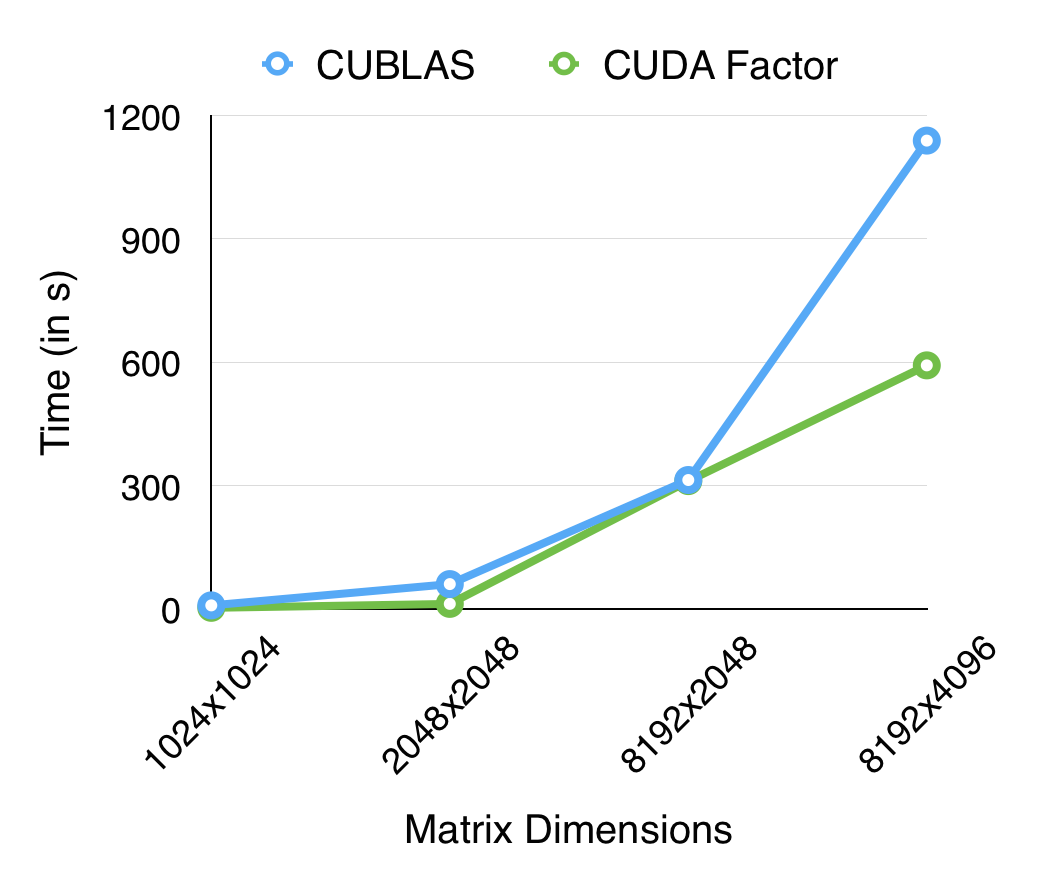
The following graph shows a comparison between our Cholesky implementation and the CULA reference when run on a Tesla K40. Our performance is comparable to the reference for smaller matrix dimensions but does not scale as well to higher matrix sizes. Optimizing this routine further is a part of the future work of this project.
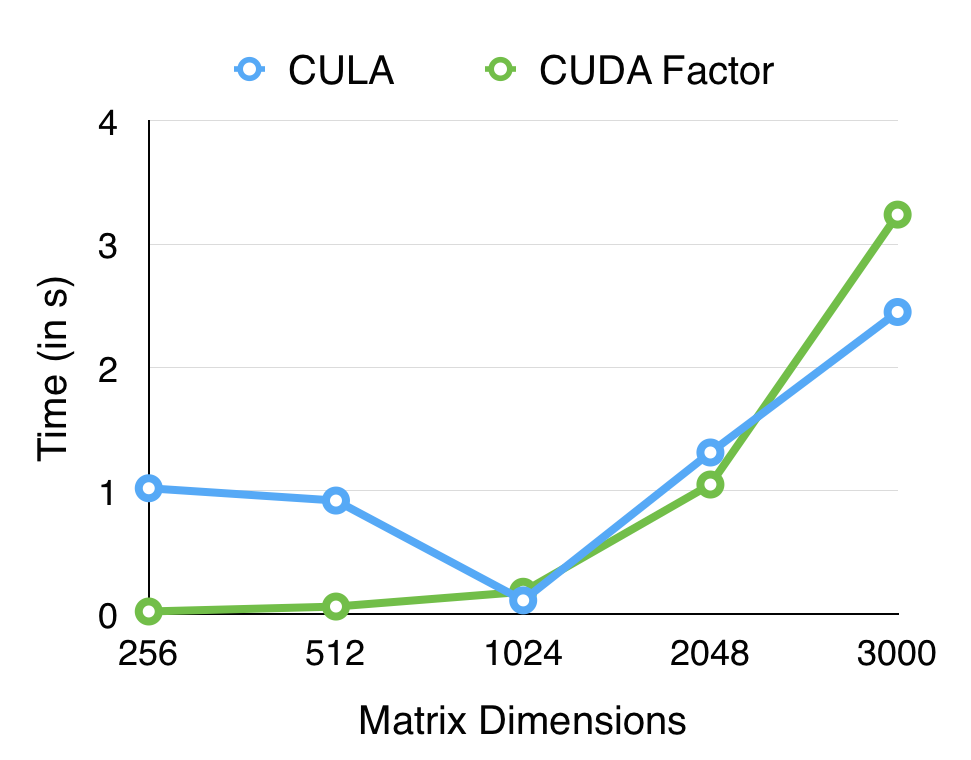
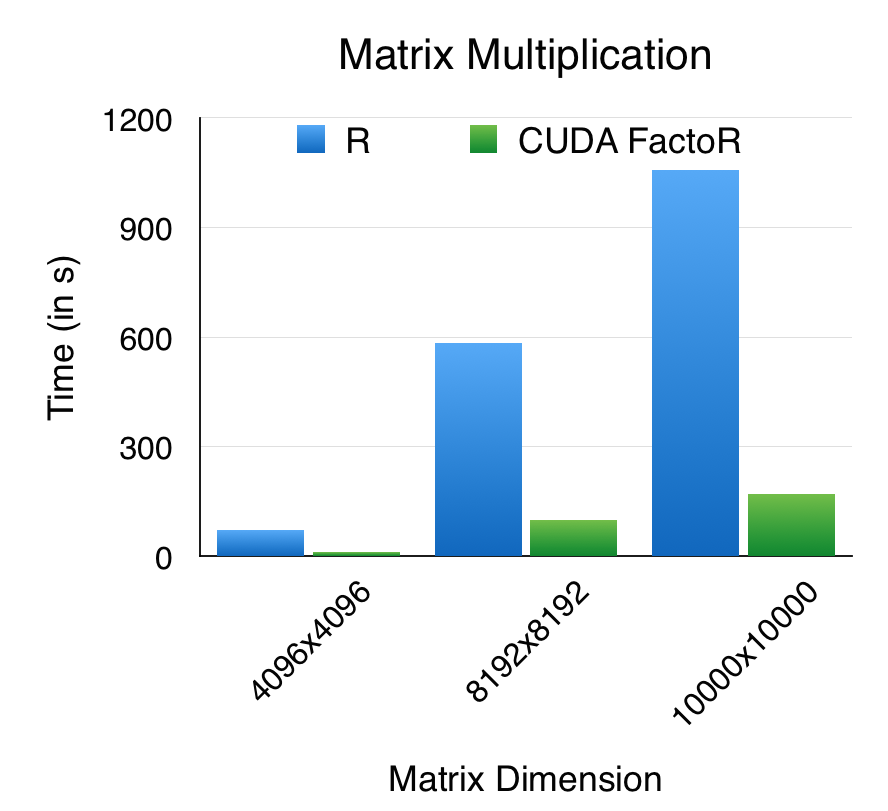
We have also designed a R interface for the Matrix Multiplication helper routine used in our source code. The comparison of this interface against R's in-built matmult() function is shown in the graph below. We would be designing similar interfaces for other routines in the future.
Writeup
Summary
We have developed a library of GPU-accelerated optimized matrix factorization routines in CUDA. The routines currently implemented are:
- LU Factorization ( A = LU )
- QR Factorization ( A = QR )
- Cholesky Factorization ( A = LLT )
Background
Matrix factorizations/decompositions are computationally intensive linear algebra operations that are commonly
used in problems like matrix inversion, solving linear systems etc. These factorizations therefore find application
in numerous fields - any place where you would solve a system of linear equations!
Domain-specific languages such as R and MATLAB have in-built functions for many matrix decompositions which are easy
to use, but are understandably very slow especially on large matrices. The aim of this project is to design a
library wherein 3 factorizations - LU, QR and Cholesky - would be implemented in CUDA and an interface to these
functions would be provided in R. Algorithms written in R which use these factorizations can benefit hugely in
terms of speedup from using this library. GPU-accelerated routines for these factorizations exist in libraries
such as cuBLAS, CULA [1] etc. which serve as reference implementations for our library.
LU Factorization
A non-singular matrix A ∈ ℜn x n is factorized into a product of lower and upper triangular matrices L ∈ ℜn x n and U ∈ ℜn x n respectively such that A = LU
A sequential "right-looking" algorithm loops over columns and updates columns to its right based on the current column [2]. The following pseudo-code describes the algorithm:
for i=1 to N /*loop over columns*/
for j= i+1 to N
A(j,i) = A(j,i)/A(i,i) /*update L*/
for k=i+1 to N
A(j,k) = A(j,k) - A(i,k)*A(j,i) /*update U*/
end
end
end
QR Factorization
A rectangular matrix A ∈ ℜm x n is factorized into a product of orthogonal and upper triangular matrices Q ∈ ℜm x m and R ∈ ℜ m x n respectively such that A = QR
One of the ways of computing the QR Factorization involves a method of applying orthogonal transformations known as "Householder reflections" [3]. Without delving into the details of the algorithm, the following pseudo-code attempts at describing the various major parts in the algorithm and their characteristics:
// Input: Matrix A
for each block /*loop over columns in blocks*/
for j = 1 to blocksize
// Find Householder vector
// Update A
end
// Initialize helper matrices Y & W
for j = 2 to blocksize
// Update Y
// Update W
end
// Update A
end
Within the scope of this project, the only important things to know about the above pseudo-code are - one, finding the householder vector involves calculating norms of vectors and two, the update A, Y & W parts consist of one or more matrix-matrix multiplications. As the size of the input matrix increases, these matrix products start becoming more and more computationally intensive. Therefore, unlike in the case of the LU factorization where data locality played an important role, here the emphasis is on matrix-matrix multiplications. Also worth noting is that within each of the for loop denoted in the pseudo-code, the iterations are not independent since the "Update" phases depend on the outputs of the previous iteration.
Cholesky Factorization
A symmetric (A = AT) and positive definite (xTAx > 0 for all x ∈ ℜ n, x ≠ 0 ) matrix A ∈ ℜn x n is factorized into a product of a lower triangular matrix L ∈ ℜn x n and its transpose such that A = LLT
Similar to the LU factorization algorithm, the sequential algorithm of the Cholesky factorization [4] has a dependency flow from left to right. In other words, the matrix columns to the right depend on the columns to the left.
for k=1 to N /*loop over columns*/
A(k,k) = √A(k,k)
for i = k+1 to N
A(i,k) = A(i,k)/A(k,k) /*update current column*/
end
for j=k+1 to N
for i=j to N
A(i,j) = A(i,j) - A(i,k)*A(j,k) /*update sub-matrix*/
end
end
end
Updating the sub-matrix is the most computation intensive part of this algorithm and hence all efforts are focused on extracting parallelism in this update. Operating over rows and columns of a matrix hints that there is data locality to be exploited in these memory accesses.
Approach
LU Factorization
We implemented a parallel version of the LU factorization algorithm on the GTX 670 GPU in the GHC machines. To begin with, the sequential algorithm was implemented using the pseudo-code in [2]. The sequential algorithm was slightly modified to enable better mapping to a GPU - this was done by separating the loops which involve updating the L and the U parts of the matrix.
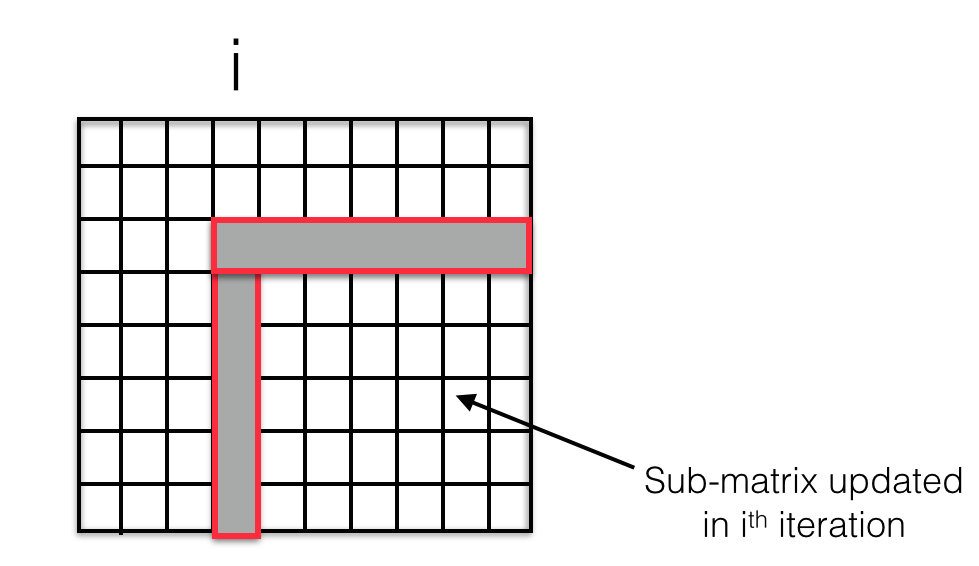
The figure above shows the part of the matrix that is updated at the ith iteration. To begin with, the most simple approach was implemented wherein each element of this sub-matrix is assigned a thread and a kernel with required number of blocks and threads per block is launched. To experiment with different memory access patterns, two other mappings were tried out. First, the sub-matrix is divided into blocks as before, but within the block only one thread per row of the block is launched (instead of one thread per element). Second, the same thing is done with columns - one thread per column of the block is launched. These two approaches characterize different memory access patterns but both have one common advantage - enabling use of shared memory. In the figure above, the row and the column shaded grey is shared by all the elements in the sub-matrix to perform their update. Hence, in a per-row or a per-column method, the part of the row and the column shared is first loaded into shared memory which is then used by all the threads within the thread block to perform their update.
QR Factorization
A parallel version of the QR factorization algorithm was implemented on the Tesla K40 in the latedays cluster as well as on the GTX 670 GPU in the GHC machines. To begin with, the sequential algorithm was implemented using the pseudo-code in [3].
As a first simple approach, we started by implementing a naive CUDA version of the Householder QR factorization. QR was much more challenging than the LU factorization especially since the sizes of the matrices involved in the "Update" phases (refer to pseudo-code above) vary every iteration. Hence, dynamic memory allocations within the for loop were abundant in the first implementation. Also, to keep things simple the householder function (which involves calculating norms) was implemented on the host side instead of the GPU. This meant a memory transfer over the bus every iteration.
Several iterations of optimizations followed this basic CUDA implementation since it wasn't close to the reference cuBLAS library implementation. The first thing which we felt could have been the bottle neck was the expensive memory transfer over the PCI-e bus every iteration. To get rid of this, the implementation of Householder function was moved to the GPU instead of the host CPU. This was done by storing the squares of the input vector (recall that the l2 norm is the square root of the sum of the squares of the elements in a vector) in an array and performing an exclusive scan on this array.
Another possible cause of the inefficiency could have been the dynamic allocation of the arrays within the loops. This overhead of allocating and freeing memory every iteration due to variable sizes could have been affecting performance was our intuition. One way to circumvent this was by taking a usual memory space v/s time trade-off. We cut down on the time spent in allocating/de-allocating memory every iteration by allocating the maximum amount of memory our code would need before the first iteration itself. The indexing within all the kernels in the loop need to be modified accordingly. This approach too did not yield desirable results and had the added drawback that due to excessive memory allocations, this implementation would break at higher matrix sizes since the device ran out of memory.
On profiling the code function-by-function, we found that the matrix-matrix multiplications - the backbone of the QR factorization routine - were the bottleneck restricting performance. Our matrix multiply kernel thus far was a naive one wherein each output element was calculated by a thread looping through the rows and columns of the input matrices. We then shifted our focus on improving our matrix multiply kernel.
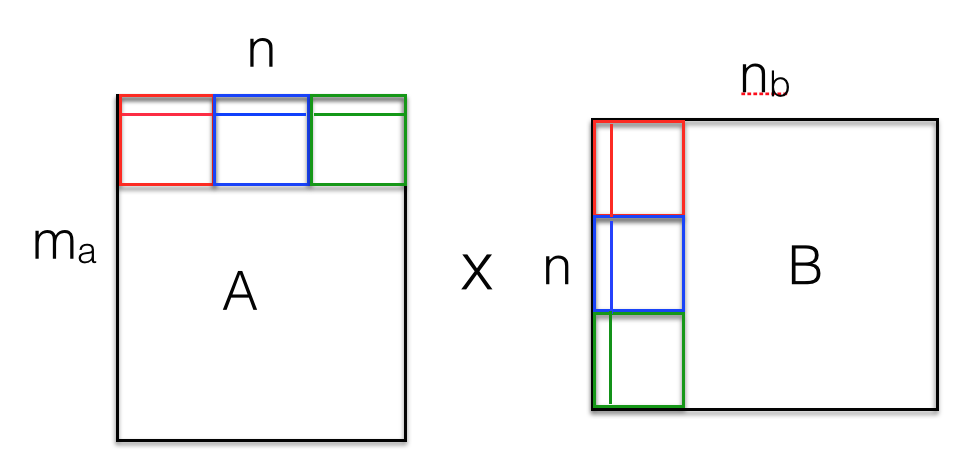
The figure above shows our approach towards optimizing matrix-matrix multiplications. Like before, one thread is launched per output matrix element. However, the kernel is now modified to make efficient use of per-block shared memory. Instead of looping through one row of A and one column of B at a time, the modified kernel follows a blocked method as shown. The blocks shown in red are first loaded into shared memory - one thread loads one element into each shared sub-matrix. We now loop through the row of the red block in A and the column of the red block in B. We do the same for the blue and the green blocks to get the output element. This approach of splitting the loop iterations into blocks makes efficient use of per-block shared memory.
Cholesky Factorization
Cholesky factorization was one of our "nice-to-haves" in the project and hence was taken on in the later phases of the project. The knowledge gained due to the LU and QR experience helped us parallelize this algorithm easily but we could not delve into detailed optimizations due to the time limitations.
We implemented a parallel version of the Cholesky factorization algorithm on the Tesla K40 in the latedays cluster. To begin with, the sequential algorithm was implemented using the pseudo-code in [4].
This application was a very good instance where modifying the initial sequential algorithm proved to be highly useful. The initial sequential Cholesky factorization algorithm we were looking at involved updating only one column at a time, contrary to the pseudo code in the previous section. This however involved scans over the rows of the input array at each iteration. This dependency limited the amount of parallelism that we could easily extract from the code. Hence, we decided to go in a different direction and hence chose the algorithm described in the pseudo-code which makes the problem similar to the LU factorization in nature.
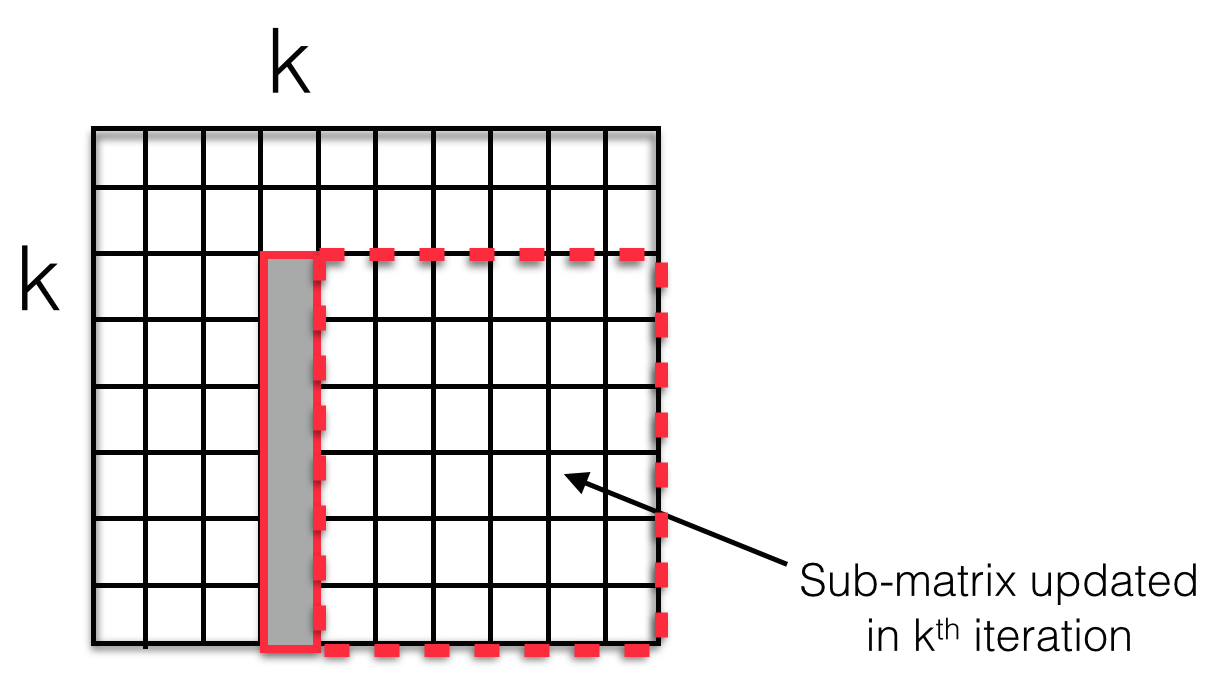
The figure above shows the part of the matrix that is updated at the kth iteration. To begin with, the most simple approach was implemented wherein each element of this sub-matrix is assigned a thread and a kernel with required number of blocks and threads per block is launched. To experiment with different memory access patterns, two other mappings were tried out. First, the sub-matrix is divided into blocks as before, but within the block only one thread per row of the block is launched (instead of one thread per element). Second, the same thing is done with columns - one thread per column of the block is launched. These two approaches characterize different memory access patterns but both have one common advantage - enabling use of shared memory. In the figure above, the column shaded gray is shared by all the elements in the sub-matrix to perform their update. Hence, in a per-row or a per-column method, the part of the column shared is first loaded into shared memory which is then used by all the threads within the thread block to perform their update.
Results
LU Factorization
The performance of our LU routine was evaluated by measuring the wall-clock time of this code and comparing it to that of the reference library. Since the cuBLAS library is in-built within newer versions of CUDA (6.0 onwards), it was the first choice of a reference implementation.
The following graph shows a comparison between our implementation and the cuBLAS reference when run on a GTX 670 GPU.

These results were obtained using the one thread per column configuration. This version performs better than the other two - one thread per element and one thread per row. To get an insight into why this is, we ran the nvprof profiler on the row and the column versions for size of input matrix N=4096. The results of this analysis are shown in the table below.
| Metric | One thread per row | One thread per column |
|---|---|---|
| gst_requested_throughput | 8.9614GB/s | 52.346GB/s |
| gld_requested_throughput | 8.1816GB/s | 55.578GB/s |
The above table shows that the average requested throughput for both global loads and stores is much higher for the one thread per column version. We believe that this is due to the cache advantage that this version offers - when one thread starts executing it loads a line into the cache, which automatically loads the data required by other threads in that thread block.
QR Factorization
The performance of our QR routine was evaluated by measuring the wall-clock time of this code and comparing it to that of the reference library. Since the cuBLAS library is in-built within newer versions of CUDA (6.0 onwards), it was the first choice of a reference implementation.
The following graph shows a comparison between our implementation and the cuBLAS reference when run on a Tesla K40.

The following graph shows a comparison between our implementation and the cuBLAS reference when run on a GTX 670 GPU.

One of the reasons for such a speedup was that the cuBLAS library focuses on performing QR factorizations on many small matrices in parallel, whereas we have focused on computing the QR factorization of a large matrix as fast as we can. We find this to be a more interesting test case since the matrices occurring in PCA computations generally tend to be higher in size. Another reason for the massive speedup as pointed out by the judges in the Parallelism Competition could be that the reference library uses a column-major order to store the matrices, whereas we have stuck with row-major order. This could also have an effect on the memory access patetrns and caching effects, though we were not able to run tests and collect data to support this hypothesis.
Cholesky Factorization
The performance of our Cholesky routine was evaluated by measuring the wall-clock time of this code and comparing it to that of the reference library. Since the cuBLAS library does not have a cholesky factorization routine, we switched to a different reference - the CULA tools library.
The following graph shows a comparison between our implementation and the CULA reference when run on a Tesla K40.

We did not have time to perform a detailed analysis on the Cholesky results since it was one of our bonus routines which we started on late in the project. However, similar to what we observed for LU, the one thread per column version was faster than the other two version for Cholesky as well; and we believe that the reasons would be the same as for LU given the similarity in the algorithms and approaches.
R Interface
One of the "nice to haves" of our project was designing a R interface for our library in order to enable the calling of some of our optimized routines from within R. Towards this end, a R wrapper was written around the CUDA helper Matrix Multiply routine and a test was created to compare the performance of the in-built matmult() function in R and the shared memory matrix multiply routine from our "CUDA Factor" library. These tests were carried out on the GTX 670 GPU in the GHC machines, which have R installed on them.

The figure above shows a significant speedup achieved especially for larger matrix sizes with respect to the in-built R function by using our library. Future work will involve writing and testing similar interfaces for other routines as well.
References
- GPU-accelerated libraries, https://developer.nvidia.com/gpu-accelerated-libraries
- Bandara, H. M. D. M., and D. N. Ranasinghe. "Effective GPU Strategies for LU Decomposition". Technical report, University of Colombo, Colombo, Sri Lanka, 2010.
- Kerr, Andrew, Dan Campbell, and Mark Richards. "QR decomposition on GPUs." Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units. ACM, 2009.
- Parallel Numerical Algorithms, Prof. Michael T. Health, University of Illinois-Urbana Champaign
Work Done
Equal work was done by both members.
Checkpoint
We have thus far made progress with LU and QR factorizations, as well as optimized matrix multiply (which was one of the "nice to haves"). To begin with, a simple sequential algorithm was implemented to compute the LU factorization. We then implemented a naive CUDA version of the same and began optimizing it. The performance of the LU factorization depends heavily on the memory access patterns and two different approaches to accessing memory were tried out. The matrix was divided into blocks and row-wise and column-wise accesses within each block were tried out. Another optimization was to use shared memory within each block to store the data which is accesses by all threads within the block.
We faced some problems initially implementing the blocked version in CUDA, mainly related to array indexing and memory accesses. We also set up benchmarks to compare our routines to. The in-built CUBLAS (CUDA Basic Linear Algebra Subroutines) library is used as a reference. However, the shared memory version of LU factorization still has some bugs and fails for higher block sizes, an issue which we are still working on. For this reason, timing the LU routine was deferred.
The implementation of the QR factorization routine was started simultaneously, which is characterized not by access patterns but by matrix-matrix and matrix-vector multiplications. Again, a sequential version was first implemeneted and then a naive CUDA one. With the naive CUDA version, our implementation is 2-3 times worse than the CUBLAS reference library for higher matrix dimensions.
| Matrix Size | CUBLAS Time | Our Time |
|---|---|---|
| 4096 x 1024 | 47.88s | 155.41s |
| 4096 x 2048 | 174.01s | 340.02s |
Because of the fact that QR Factorization has many matrix-matrix multiplications, it makes sense for us to focus on one of our "nice to haves" - the matrix multiplication routine - and optimize it at this stage. One of the optimizations which we think will improve our run time performance of the QR routine is to modify the algorithm slightly so that the memory allocations are optimal. Another major one would be to use optimized matrix multiply routine instead of the naive one which we have currently written.
Finally, we believe that we would be able to produce a library with at least 3 fast and efficient matrix routines - LU factorization, Matrix Multiply and QR factorization. If all goes as planned, we think that the other "nice to have" - Cholesky decomposition - is also within reach for us, before the deadline. For the Parallelism Competition, we will display a comparison of our implementation with respect to the CUBLAS library in the form of a graph.
Proposal
Summary
We will be developing a library of GPU-accelerated optimized matrix factorization routines in CUDA.
Background
The factorization routines focused on in this project are LU and QR (and, if time permits, Cholesky) Factorization. Both these function involve splitting a given matrix into a product of two matrices.
LU Factorization
LU Factorization involves splitting a regular NxN matrix A into a product of a lower triangular matrix L and an upper triangular matrix U using Gaussian elimination. This factorization finds applications in simplifying linear algebra operations such solving a system of linear equations Ax = b, calculating the determinant of a matrix, inverting a matrix etc.
A sequential "right-looking" algorithm loops over columns and updates columns to its right based on the current column. The following pseudo-code describes the algorithm:
for i=1 to N /*loop over columns*/
for j= i+1 to N
A(j,i) = A(j,i)/A(i,i) /*update L*/
for k=i+1 to N
A(j,k) = A(j,k) - A(i,k)*A(j,i) /*update U*/
end
end
end
QR Factorization
QR factorization splits a rectangular MxN matrix A into two matrices Q and R such that A=QR. Here, Q is a MxM orthogonal matrix whereas R is a NxN upper triangular matrix. This decomposition too is very useful in finding solutions to a system of linear equations. QR decomposition is also widely used to solve the linear as well as the nonlinear least squares problem.
The algorithm to decompose a matrix into QR factors is based on the so called Givens rotations which are orthogonal. Using a sequence of givens rotations the given matrix can be transformed to an upper triangular matrix. Givens rotations can be systematically applied to successive pairs of rows of matrix A to zero entire strict lower triangle. Parallelizing the computation of Givens rotations is one avenue but there could also exist an opportunity to parallelize the step of applying this transformation to pairs of rows.
Challenge
LU Factorization
The sequential algorithm for the LU decomposition will have to be modified in order to efficiently parallelize it. The data dependencies in the algorithm in outermost loop will have to be dealt with. The algorithm in its current form, does not have independent outer loop iterations. Also, the 3 different loops within a matrix imply that there are different access patterns possible and an efficient implementation will use one which best exploits locality. The challenging part would be to implement a parallel version of the algorithm which best takes advantage of the locality in the problem and efficiently uses GPU resources such as shared memory. Thus, the problem should be an interesting opportunity to apply platform-specific and application-specific optimizations.
QR Factorization
The challenge in this routine is to come up with an algorithm which reduces the amount of synchronization needed. The idea is to exploit parallelism in as many steps of the algorithm as we can by efficiently implementing it on a GPU.
Resources
We will be using a GPU on one of the GHC machines. The references for the LU and QR Factorization are cited as [1] and [2] respectively.
Goals and Deliverables
The goal of the project is to develop a fast library in CUDA to implement atleast two matrix factorization routines.
We expect to deliver an efficient, highly optimized implementation of the two routines on an NVIDIA GPU. Moreover, if time permits, we would also extend our project to include a similar efficient implementation of Cholesky Factorization. Matrix multiplication is another application we would like to implement as a part of the library. Though not a decomposition routine, we believe it would be a good challenge to implement a optimized matrix multiplication routine as near in performance as possible to state-of-the-art implementations. The performance of the library will be measured by plotting speedup graphs and comparing them with state-of-the-art libraries. Another extension is to provide a R interface to these optimized CUDA routines, which was the original inspiration behind the project - making R code faster by GPU acceleration.
Platform Choice
GPUs are suitable for matrix operations since they offer a huge amount of data parallelism.
Original Schedule
| Day | Planned Work |
|---|---|
| April 6 | Finalize proposal, Research efficient implementations |
| April 13 | Optimized LU Factorization routine |
| April 20 | Basic QR Factorization routine |
| April 27 | Optimize QR Factorization |
| May 4 | Cholesky/Matrix Multiply |
| May 11 | Finish final report and prepare presentation |
New Schedule
| Day | Planned Work |
|---|---|
| April 6 | Finalize proposal, Research efficient implementations, Sequential LU |
| April 13 | 3 approaches for LU Factorization, some bugs with shared memory |
| April 20 | Sequential QR Factorization routine and naive CUDA implementation |
| April 24 | Optimize Matrix Multiply, Fix shared memory LU (Ravi) |
| April 27 | QR Factorization - optimal allocations (Harsha) |
| May 1 | Optimize QR - shared memory |
| May 4 | Benchmark results and Cholesky decomposition |
| May 7 | Optimize Cholesky and finish any pending work |
| May 11 | Finish final report and prepare presentation |
References
- Bandara, H. M. D. M., and D. N. Ranasinghe. "Effective GPU Strategies for LU Decomposition". Technical report, University of Colombo, Colombo, Sri Lanka, 2010.
- Kerr, Andrew, Dan Campbell, and Mark Richards. "QR decomposition on GPUs." Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units. ACM, 2009.